Projections cartographiques et sytèmes de coordonnées Même si l'utilisation de récepteurs GPS a énormément gagné en convivialité ces dernières années, l'interprétation des valeurs obtenues peut poser quelques difficultés aux non-initiés. Voici donc un petit apperçu des notions de bases en géodésie/géomatique pour surmonter cette barrière psychologique!

Geoïde La finalité d'une "mesure" avec un récepteur GPS est de déterminer avec précision une position sur la surface du globe. Le récepteur GPS produit donc une série de valeurs numériques que l'on doit corréler (par un modèle quelconque) à un "endroit" sur la Terre (ou dans les airs). La première difficulté apparaît lorsque l'on regarde de près la forme de la Terre. Elle n'est pas plate (et pourtant ça aurait été bien pratique), ni ronde, ... elle a une forme irrégulière. Cette forme c'est ce que l'on nomme "la géoïde", définie plus précisément comme le niveau moyen des mers. Notez que la géoïde fait déjà abstraction du relief, c'est en fait la surface de base à partir de laquelle on définit l'altitude (altitude orthométrique). Ainsi, par définition et très logiquement, le niveau moyen des mers est à l'altitude 0. 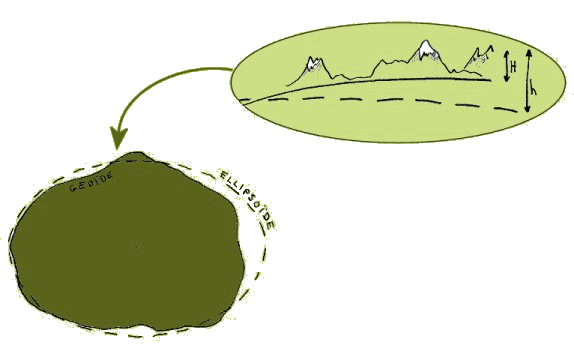Figure 3.1: Représentation de la géoïde et d'une ellipsoïde de référence. Le détail montre la différence entre l'altitude orthométrique (H) et ellipsoïdale (h).

Les Systèmes de Référence D'un point de vue mathématique la géoïde est une surface qui ne peut pas être décrite de manière simple, avec quelques paramètres. Par contre elle ressemble à une ellipse de révolution, qui elle est un objet mathématiquement bien plus sympathique. A partir du moment ou l'éllipse est choisie et les axes de référence fixés par rapport à la Terre, il suffi de 2 paramètres (latitude/longitude) pour déterminer un endroit sur l'ellipse, et un troisième paramètre si on veut s'élever par rapport à cette ellipse (altitude ellipsoïdale). Ces trois valeurs constituent les coordonnées géographiques d'un point. L'ensemble ellipse positionnée + axes de références constitue un CTRS (Conventional Terrestrial Reference System), l'un des plus important étant l'ITRS (International Terrestrial Reference System). Ce dernier est ajusté régulièrement (2 à 3 ans) afin d'obtenir la meilleure précision possible. Mais vous vous en doutez il y a d'autre systèmes (Datum) définis à divers époques par divers institutions ... Les ellipses de références peuvent varier dans leur taille (grand axe, petit axe) ou/et leur positionnement par rapport au centre de la terre. Ainsi les coordonnées géographiques d'un lieu varient en fonction du choix de l'ellipse de référence. Pour cette raison les coordonnées géographiques sont toujours accompagnées du système de référence choisi. I 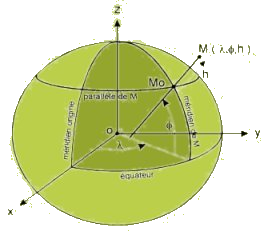Figure 3.2: Coordonnées géographique latitude (phi),longitude (lambda) et altitude (h). Le système GPS est basé sur un système géocentrique, WGS84 (World Geodetic System 1984), développé par la DMA (US Defense Mapping Agency). Le WGS84 est très proche (quelques milimètres) des dernières évolutions du système ITRF.

Projections cartographiques Pour représenter la surface du globe sur une carte plane, et pour avoir des positions en fonction de coordonnées plus simples à utiliser que les données angulaires (latitude/longitude) il faut passer par une projection. La carte ainsi obtenue représente la surface de la Terre dans une grille rectangulaire, les coordonnées sont appelée easting (x) et northing (y). Cette transformation n'est pas triviale puisque la sphère n'est pas une surface développable. En d'autres termes on ne peut pas transformer une surface sphérique en un plan sans « étirer » et/ou « contracter » certaines régions. Une carte est donc toujours une présentation déformée de la réalité. Il existe de très nombreuses projections, que l'on peut classer en trois catégories : Les projections conformes, qui conserve les angles Les projections équivalentes, qui conservent les aires Les projections aphylactiques, qui sont un compromis entre les deux précédantes et qui ne conservent ni les angles, ni les aires Voici quelques-unes des projections courantes classées par le type de surface développable utilisée. Figure 3.3: Principales surfaces de projection, plan, cone, cylindre   Projections sur un plan : azimutales Ce sont les projections généralement utilisées pour représenter les pôles. 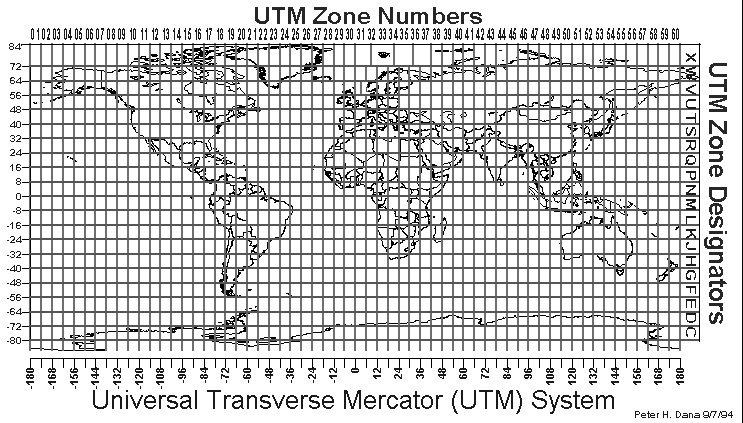Exemple : projection gnomique, Lambert azimutales Figure 3.4: Exemple de projection Lambert azimutale Projections sur un cône : coniques La surface de projection est un cône qui est soit tangent soit sécant au globe. Elles peuvent être conformes ou équivalentes, les déformations sont constantes sur une latitude donnée. Exemples : projection conique de Lambert, projection d'Albert Projections sur un cylindre : cylindriques C'est la famille de projections la plus variée, le cylindre est soit tangent soit sécant à la sphère. La projection la plus utilisée, dite de Mercator, utilise un cylindre tangent à l'équateur et dont l'axe est parallèle à l'axe des pôles, c'est une représentation conforme. La projection de Peters utilise le même cylindre développable, mais elle est équivalente. D'autres variantes sont basées sur un cylindre dont l'axe est perpendiculaire à l'axe des pôles, ce sont les projections transverses (Mercator Transverse appelée aussi Gauss-Krügger et inventée par l'allemand Johann Lambert [1772]). La plus usitée, la projection UTM (Universal Transverse Mercator), divise la terre en 60 zones correspondant à la rotation progressive de l'axe du cylindre autour de l'axe des pôles. En sciences de la terre les données sont généralement réprésentées dans la projection de Mercator, les raisons sont historiques puisque c'est le type de projection traditionnellement utilisée pour les cartes marines, disponibles lors des premières expéditions scientifiques. Figure 3.5: Projection de Mercator Revenons un peu sur la célèbre projection UTM. Il s'agit donc d'une projection conforme transverse de l'ellipsoïde. La Terre est divisée en 60 fuseaux de 6°, le cylindre de projection est sécant et il est progressivement tourné et aligné au méridien central de chacun des fuseaux. Pour éviter des coordonnées négatives l'origine de chaque fuseau (intersection du méridien central et de l'équateur) est fixé par définition à la position : x = 500'000 et y = 0 pour l'hémisphère Nord (y = 10'000'000 pour l'hémisphère Sud). Le facteur d'échelle au niveau du méridien central de la zone est de 0.9996. Ce facteur permet d'avoir une déformation plus uniforme avec en bord de zone une échelle à 1.00097. Figure 3.6: Zones UTM

Systèmes locaux Pour la représentation d'une zone limitée sur le globe, le choix d'une ellipsoïde géocentrique n'est pas forcément très judicieux. Ainsi chaque pays a développé son système de référence local basé sur une ellipsoïde ajustée à la région. PAYS REALISATION ELLIPSOIDE Suisse CH1903 France NTF

Chapitre précédant - Chapitre suivant

Bibliographie Introduction to GPS - The global positioning system, Ahmed El-Rabbany, 2002 Artech House INC., 685 Canton Street, Norwood MA 02062. Geodesy: The Concepts - Vanicek P. and E.J. Krakiwsky, 1986 New York: North Holland Formes et Mouvements de la Terre, Satellites et géodésie - Cazenave A, Feigl K, 1994 Berlin. Institut Géographique National, www.ign.fr

Retour à la Table des Matières